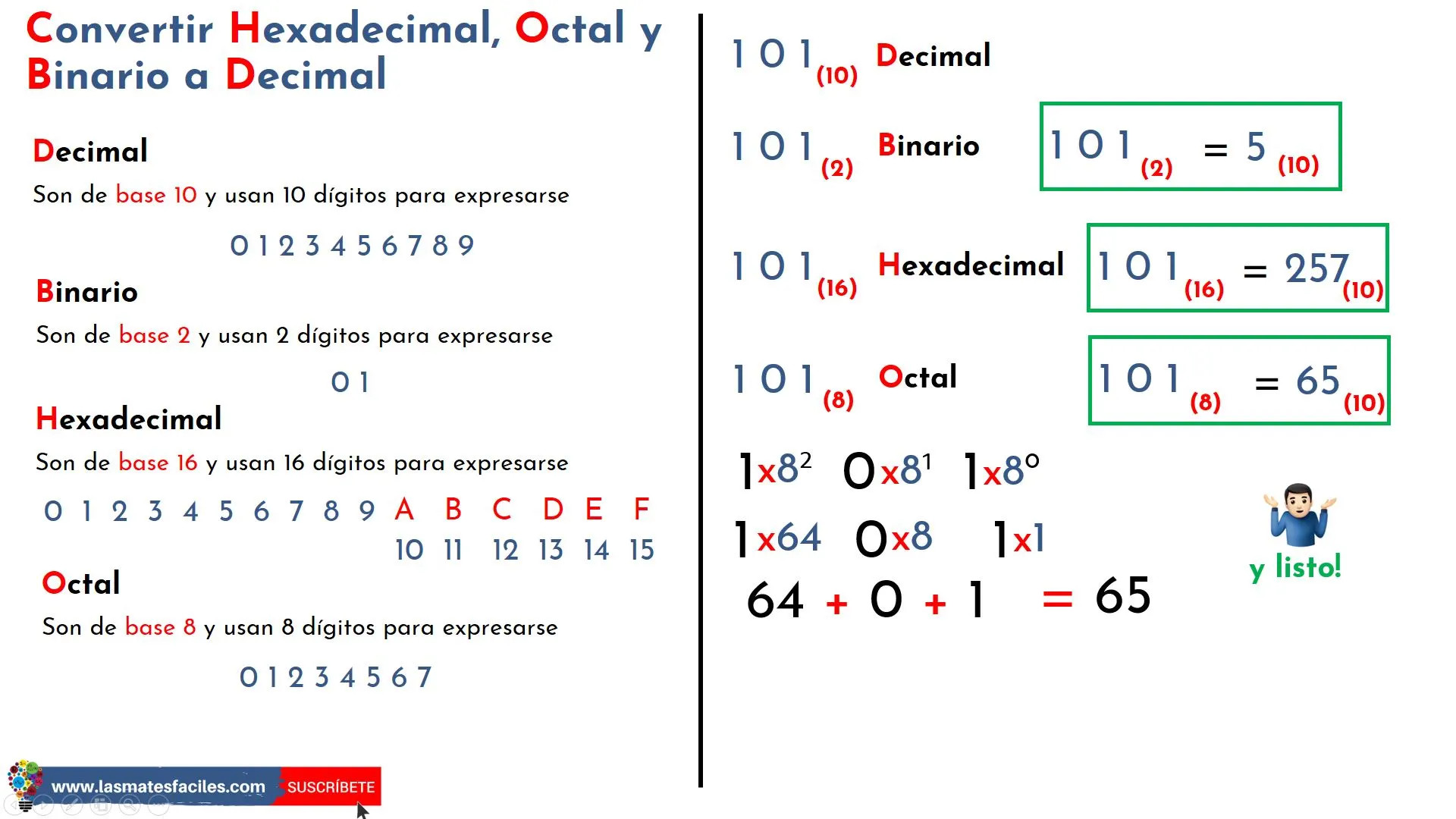
1. Sistema Decimal: Utiliza diez símbolos (0 al 9) y se basa en potencias de diez. Es el sistema que utilizamos habitualmente en nuestra vida diaria.

2. Sistema Binario: Utiliza dos símbolos (0 y 1) y se utiliza principalmente en computación y electrónica.

3. Sistema Octal: Utiliza ocho símbolos (0 al 7) y se usa ocasionalmente en programación y matemáticas.

4. Sistema Hexadecimal: Utiliza dieciséis símbolos (0 al 9 y A a F) y es común en programación y en la representación de colores.

CONCLUSIONES 

El sistema de numeración en computación se basa principalmente en el sistema binario (base 2), aunque también se utilizan otros sistemas como el octal (base 8) y el hexadecimal (base 16) por razones prácticas. Aquí están algunas conclusiones clave sobre el sistema de numeración en computación

https://www.youtube.com/watch?v=8aqdm68RC04

Operaciones en Sistemas Numéricos

1. Suma y Resta:

   • Realizar las operaciones directamente en el sistema numérico correspondiente, teniendo en cuenta los acarreos y préstamos necesarios en cada caso.

2. Multiplicación:

   • Multiplicar como en el sistema decimal, pero teniendo en cuenta la base del sistema numérico en el que se está operando.

3. División:

   • Realizar la división como en el sistema decimal, adaptando los procedimientos a la base numérica del sistema en uso.

Importancia y Aplicaciones

• Las conversiones entre sistemas numéricos son esenciales en computación, programación y electrónica para la manipulación eficiente de datos.
• Las operaciones en diferentes bases numéricas permiten realizar cálculos específicos que pueden ser críticos en el diseño y la optimización de algoritmos.
• Entender y aplicar estas conversiones y operaciones ayuda a los profesionales en tecnología a desarrollar software eficiente y a comprender mejor los fundamentos de los sistemas digitales.

CONCLUSIONES

1. Flexibilidad y Adaptabilidad:

   • La capacidad de convertir entre diferentes sistemas numéricos (decimal, binario, hexadecimal, octal, etc.) permite representar datos de manera eficiente según las necesidades del contexto, como en programación o diseño de circuitos.

2. Optimización y Eficiencia:

   • Operar directamente en sistemas de numeración alternativos (como binario u octal) puede ser más eficiente para ciertas aplicaciones computacionales y electrónicas, dado que reflejan mejor la estructura interna de los dispositivos digitales.

3. Precisión y Exactitud:

   • Las conversiones y operaciones en sistemas de numeración deben realizarse con precisión para evitar errores de cálculo que podrían afectar el funcionamiento de los sistemas electrónicos y software.

4. Aplicaciones Específicas:

• Cada sistema numérico tiene aplicaciones específicas. Por ejemplo, el binario es esencial en la representación de datos en computadoras y electrónica, mientras que el hexadecimal se utiliza frecuentemente en programación debido a su concisión para representar grandes números binarios.

ENLACE DE VIDEO:

https://www.youtube.com/watch?v=4kenXkQBIEw&list=PL46-B5QR6sHleyaafOF3Vp1ZpiUEtHJ40